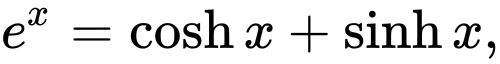mathematical function related with trigonometric functions
Wikipedia
en.wikipedia.org › wiki › Hyperbolic_functions
Hyperbolic functions - Wikipedia
3 weeks ago - sinh(x) and cosh(x) are also the unique solution of the equation f ″(x) = f (x), such that f (0) = 1, f ′(0) = 0 for the hyperbolic cosine, and f (0) = 0, f ′(0) = 1 for the hyperbolic sine.
WebConversionOnline
webconversiononline.com › trigonometry-calculator.aspx
Value of CosH(0) - Hyperbolic Cosine
Find value of CosH(0) - Hyperbolic Cosine or Calculate value of Sin, Cos, Tan, Cot, Cosec, Sec, SinH, CosH, TanH, CotH, CosecH, SecH, ASin, ACos, ATan, ACot, ACosec, ASec and other trigonometry function
Videos
Mathway
mathway.com › popular-problems › Trigonometry › 337398
Find the Exact Value cos(h(0)) | Mathway
Find the Exact Value cos(h(0)) I am unable to solve this problem. Please ensure that your password is at least 8 characters and contains each of the following: a number ·
Homework.Study.com
homework.study.com › explanation › find-the-numerical-value-of-cosh-0.html
Find the numerical value of cosh 0. | Homework.Study.com
Rewrite the expression in terms of exponentials and simplify the results. 6 cosh (ln x) if X''- 4x = 0; then { m^2- (4) = 0 ,m =_ +^- 2 } which should be { e^{(2x)} + e^{(-2x)} } how is that cosh (2x) + sinh (2x)
Mathcentre
mathcentre.ac.uk › resources › workbooks › mathcentre › hyperbolicfunctions.pdf pdf
Hyperbolic functions
The function satisfies the conditions sinh 0 = 0 and sinh(−x) = −sinh x. The graph of sinh x ... We can see this by sketching the graphs of sinh x and cosh x on the same axes. ... For large values of x the graphs of sinh x and cosh x are close together. For large negative · values of x the graphs of sinh x and −cosh x are close together. ... We shall now look at the hyperbolic function tanh x.
University of Connecticut
www2.math.uconn.edu › ~stein › math115 › Slides › math115-180notes.pdf pdf
Derivatives of Trigonometric Functions
Since limh→0 cos h = limh→0 · 1 · cos h = 1, by the Squeeze Theorem it · follows that limh→0 · sin h · h · = 1 · QED · Claim 2. limh→0 · 1 −cos h · h · = 0. We make use of the identity involving sin and an algebraic manip- ulation reminiscent of rationalization, enabling ...
Whitman College
whitman.edu › mathematics › calculus_online › section04.11.html
4.11 Hyperbolic Functions
Definition 4.11.1 The hyperbolic cosine is the function $$\cosh x ={e^x +e^{-x }\over2},$$ and the hyperbolic sine is the function $$\sinh x ={e^x -e^{-x}\over 2}.$$ $\square$ Notice that $\cosh$ is even (that is, $\cosh(-x)=\cosh(x)$) while $\sinh$ is odd ($\sinh(-x)=-\sinh(x)$), and $\ds\cosh x + \sinh x = e^x$. Also, for all $x$, $\cosh x >0$, while $\sinh x=0$ if and only if $\ds e^x -e^{-x }=0$, which is true precisely when $x=0$. Lemma 4.11.2 The range of $\cosh x$ is $[1,\infty)$. $\square$ Proof.
Mathway
mathway.com › popular-problems › Calculus › 572074
Evaluate the Limit ( limit as h approaches 0 of cos(h))/h | Mathway
Evaluate the Limit ( limit as h approaches 0 of cos(h))/h · Step 1 · Move the limit inside the trig function because cosine is continuous. Step 2 · Evaluate the limit of by plugging in for . Step 3 · The exact value of is . Please ensure that your password is at least 8 characters and contains each of the following: a number ·
Mathway
mathway.com › popular-problems › Calculus › 551716
Determine the Type of Number cos(h(0)) | Mathway
Determine the Type of Number cos(h(0)) I am unable to solve this problem. Please ensure that your password is at least 8 characters and contains each of the following: a number ·
Programiz
programiz.com › c-programming › library-function › math.h › cosh
C cosh() - C Standard Library
long double coshl( long double arg); float coshf( float arg); #include <stdio.h> #include <math.h> int main () { double x, result; x = 0.5; result = cosh(x); printf("Hyperbolic cosine of %lf (in radians) = %lf\n", x, result); x = -0.5; result = cosh(x); printf("Hyperbolic cosine of %lf (in radians) = %lf\n", x, result); x = 0; result = cosh(x); printf("Hyperbolic cosine of %lf (in radians) = %lf\n", x, result); x = 1.5; result = cosh(x); printf("Hyperbolic cosine of %lf (in radians) = %lf\n", x, result); return 0; }
Mathematics LibreTexts
math.libretexts.org › bookshelves › calculus › map: university calculus (hass et al.) › 7: integrals and transcendental functions
7.3: Hyperbolic Functions - Mathematics LibreTexts
November 10, 2020 - Also, \(\sinh x > 0\) when \(x>0\), so \(\cosh x\) is injective on \([0,\infty)\) and has a (partial) inverse, \(\text{arccosh} x\). The other hyperbolic functions have inverses as well, though \(\text{arcsech} x\) is only a partial inverse.
Reddit
reddit.com › r/learnmath › cos(h) - 1)/h = 0 proof
r/learnmath on Reddit: cos(h) - 1)/h = 0 proof
August 2, 2024 -
https://www.canva.com/design/DAGgkeR10n8/6x2-gkZZI9VVdNR4QtmDKw/edit?utm_content=DAGgkeR10n8&utm_campaign=designshare&utm_medium=link2&utm_source=sharebutton
It will help if someone could confirm the way (cos(h) - 1)/h = 0 proved correct or not.
Top answer 1 of 3
4
The diagrams are a rather messy and I can't tell exactly what you are trying to do. Generally proofs should be written in complete sentences. Your proof seems to assume that cos(h) has a constant value of 1 around h=0. This would be sufficient to prove that the limit is zero, but the assumption would be false. Proofs of facts like this will ultimately rely on what definition of sine and cosine your text is using
2 of 3
3
Your proof is incorrect.
Math10
math10.com › en › algebra › hyperbolic-functions › hyperbolic-functions.html
Hyperbolic Functions - sinh, cosh, tanh, coth, sech, csch
The following list shows the principal values [unless otherwise indicated] of the inverse hyperbolic functions expressed in terms of logarithmic functions which are taken as real valued. $\sinh^{-1} x = \ln(x + \sqrt{x^2 + 1})$ $-\infty < x < \infty$ $\cosh^{-1} x = \ln(x + \sqrt{x^2 - 1})$ $x \geq l$ [$\cosh^{-1} x > 0$ is principal value] $\tanh^{-1} x = \frac{1}{2} \ln\frac{(1 + x)}{(1 - x)}$ $- 1 < x < 1$ $\coth^{-1} x = \frac{1}{2} \ln\frac{(x + 1)}{(x - 1)}$ $x > 1$ or $x < -1$ $\text{sech}^{-1} x = \ln(\frac{1}{x} + \sqrt{\frac{1}{x^2} - 1})$ $0 < x \leq l$ [$\text{sech}^{-1} x > 0$ is principal value] $\text{csch}^{-1} x = \ln(\frac{1}{x} + \sqrt{\frac{1}{x^2} + 1})$ $x \neq 0$ csch-1 x = sinh-1 (1/x) sech-1 x = cosh-1 (1/x) coth-1 x = tanh-1 (1/x) sinh-1(-x) = -sinh-1x ·
Reddit
reddit.com › r/mathhelp › [limits & derivatives] how did the remove the h and solve [(cosh-1)/h]? i don't get it [help] [see pic]
r/MathHelp on Reddit: [Limits & Derivatives] How did the remove the h and solve [(cosh-1)/h]? I don't get it [HELP] [See Pic]
July 30, 2021 -
Image - https://imgur.com/a/fdYnmdH
How did they solve for (cosh-1)/h
How did they remove the denominator h?
Kindly clear my doubt
Top answer 1 of 3
2
Lim x → 0 [(cos(x) - 1) / x] = 0 It's an identity (that is typically proven by geometry, I think. I'm more a computer guy, haven't learned a lot of geometry) that they just need you to kinda accept is true in a calculus class. The only calc way I can think to prove it is L'Hopital... Which feels like cheating because you actually run into this limit when proving the derivatives of trig functions. So its kinda like using the answer to prove your answer (because L'Hopital uses the derivative of the numerator and denominator to simplify the limit), but L'Hopital gives:) Lim x → 0 [(cos(x) - 1) / x] = Lim x → 0 [{(d/dx) (cos(x) - 1)} / {(d/dx) x}] = Lim x → 0 [(-sin(x) - 0) / 1] = -sin(0) = 0 Other major instances of identities that they either don't usually prove, or don't really deep dive in calc 1, that are good to know: Lim x → 0 [(sin(x))/x] = 1 Lim x → ∞ [{1 + (1/x)}x ] = e Lim x → 0 [(1 + x)1/x ] = e That last one is incredibly useful if you end up needing to prove, by the limit definition of a derivative, that d/dx ex = ex . (Same for d/dx ln(x) = 1/x) (Also, as a sidenote, there is a function cosh(x) which is the hyperbolic cosine. But here, cos(h) is just the cosine of h (not the hyperbolic cosine). Incase you've been trying to Google this issue and been getting answers about cosh instead.)
2 of 3
1
This is an automated reminder: What have you tried so far? (See Rule #2; to add an image, you may upload it to an external image-sharing site like Imgur and include the link in your post.) Please don't delete your post. (See Rule #7) We, the moderators of r/MathHelp , appreciate that your question contributes to the MathHelp archived questions that will help others searching for similar answers in the future. Thank you for obeying these instructions. I am a bot, and this action was performed automatically. Please contact the moderators of this subreddit if you have any questions or concerns.
UCI Mathematics
math.uci.edu › ~ndonalds › math2a › notes › 3-3.pdf pdf
cos h sin h tan h 1 h h
as h →0 of the following difference quotient: f (x + h) −f (x) h · = sin(x + h) −sin x · h · = sin x cos h + cos x sin h −sin x · h · (multiple-angle formula) = sin xcos h −1 · h · + cos xsin h · h · If our guess above is correct, then we need to prove the following: Theorem.