The quantile or probit function, as you can see from the link (see "Computatuon"), is computed with inverse gaussian error function which I hope is downloadable for calculators like TI-89. Look here for instance.

(1) The first quartile of standard normal distribution is -0.67 . (2) The third quartile of standard normal distribution is 0.67 . (3) The percentage of the observations in the standard normal distribution that are suspected outliers is, 0.74% . Explanation: A standard normal distribution has mean 0 and variance 1. ( 1 ) The first quartile of any data is the value below which 25% of the data lie. That is, P (Z < z) = 0.25. The value of z is -0.67 . Thus, the first quartile of standard normal distribution is -0.67 . ( 2 ) The third quartile of any data is the value below which 75% of the data lie. That is, P (Z < z) = 0.75. The value of z is 0.67 . Thus, the third quartile of standard normal distribution is 0.67 . ( 3 ) In case of a standard normal distribution values lying outside the range (Q₁ - 1.5 IQR, Q₃ + 1.5 IQR) are considered as outlier. Compute the range as follows: tex=[-0.67-(1.5\times 1.34),\ -0.67+(1.5\times 1.34)]\\=[-2.68, 2.68][/tex] Compute the probability of ( Z < -2.68) and P ( Z > 2.68) as follows: [tex]P(Z<-2.68)=1-P(Z<2.68)=1-0.9963=0.0037[/tex] [tex]P(Z>2.68)=1-P(Z<2.68)=1-0.9963=0.0037[/tex] The probability of a value being an outlier is, P (Outlier) = P (Z < -2.68) + P (Z > 2.68) = 0.0037 + 0.0037 = 0.0074 The percentage of the observations in the standard normal distribution that are suspected outliers is, 0.0074 × 100 = 0.74% .

Look at a table of the standard normal distribution.

At what values of z it is $\Phi(z)=0.25, \Phi(z)=0.50$ or $\Phi(z)=0.75$ ?

The values of z are the quartiles $Q_1,Q_2$ and $Q_3$.

You may be confusing population quantiles with the sample quantiles that estimate them. Your population quantiles are appropriately represented in your figures.

Population quantiles. If random variable $X \sim \mathsf{Norm}(\mu = 100, \sigma = 15),$ then quantiles $.01, .05, .25, .50, .95, .99$ of the distribution can be found in R by using the quantile function qnorm. (The quantile function is sometimes called the 'inverse CDF` function.)

q = round(qnorm(c(.01,.05,.25,.50,.75,.95,.99), 100, 15),3);  q
[1]  65.105  75.327  89.883 100.000 110.117 124.673 134.895 

These quantiles (at vertical lines) can be displayed along with the density function of $\mathsf{Norm}(100, 15)$ as shown in the graph below.

 curve(dnorm(x, 100, 15), 50, 150, col="blue", lwd=2, ylab="PDF",
      main="Density of NORM(100, 15) with Various Quantiles")
   abline(h=0, col="green2");  abline(v=0, col="green2")
   abline(v=q, col="red", lty="dotted", lwd=2)

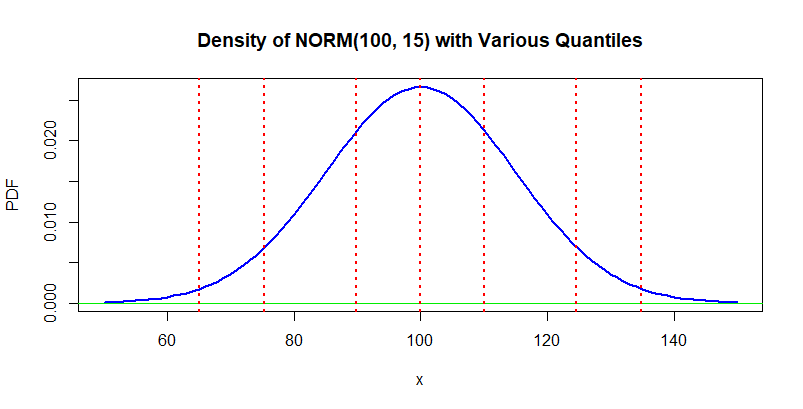
The total area (representing probability) under the density curve is $1.$ Areas to the left of the three left-most vertical lines are $.01,.05,$ and $.25,$ respectively.

Sample quantiles. If I have a sufficiently large sample from this distribution, then I can find the quantiles of the sample. For example, the 50th sample percentile (quantile .5) is the sample median. These sample quantiles estimate the corresponding population percentiles. Generally speaking, larger samples give better estimates. I will use $n = 1000$ in my example.

set.seed(2020) # for reproducibility
x = round(rnorm(1000, 100, 15), 3)

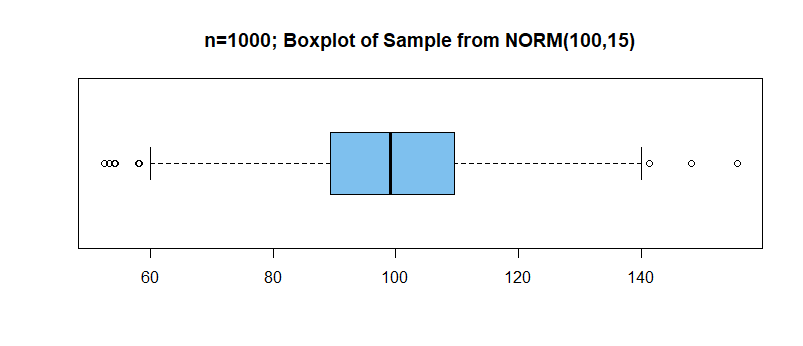
Here are some summary statistics of the sample, including the sample first quartile (quantile .25), the sample median, and the sample third quartile (quantile .75). The boxplot uses the quartiles [upper and lower edges of the box]and the median [center line inside box], so we show it also.

summary(x)
    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   52.51   89.30   99.14   99.60  109.58  155.54 

boxplot(x, col="skyblue2", horizontal=T,
        main="n=1000; Boxplot of Sample from NORM(100,15)")

Without extra arguments, the R procedure quantile shows the maximum and minimum values in the sample and the three quantiles shown in the summary.

quantile(x)
       0%       25%       50%       75%      100% 
 52.50800  89.30475  99.13750 109.57850 155.54300 

In order to get our full list of quantiles, we need to specify them individually.

samp.q = quantile(x, c(.01,.05,.25,.50,.75,.95,.99));  samp.q
       1%        5%       25%       50%       75%       95%       99% 
 63.76255  74.46450  89.30475  99.13750 109.57850 126.38775 136.60263 

In particular, notice that population quantile .05 (which is $75.327$ from earlier) is estimated by the sample quantile .05 (which is $74.465$ just above).

Finally, we show a histogram of the $n=1000$ observations along with the population density curve. Now the vertical dotted lines show the positions of our chosen sample quantiles.

hist(x, prob=T, col="skyblue2", main="Histogram of Sample")
 curve(dnorm(x, 100, 15), add=T, col="blue", lwd=2)
 abline(v=samp.q, col="purple", lty="dotted", lwd=2)

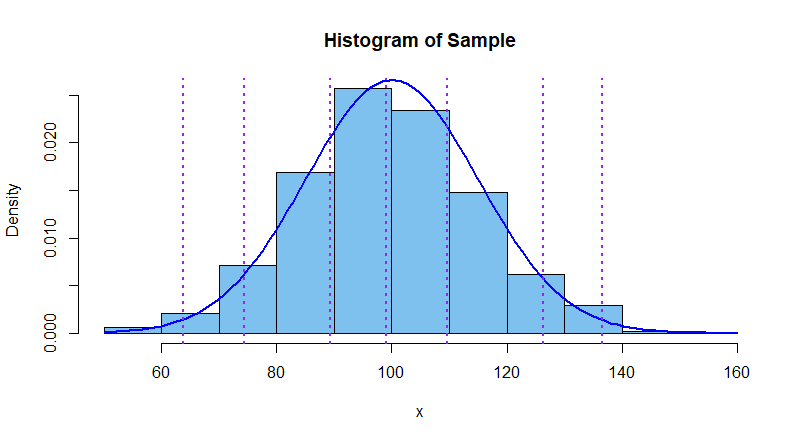
Numbers of observations at or to the left of the three left-most vertical lines are $10, 50,$ and $250,$ respectively, out of $1000.$

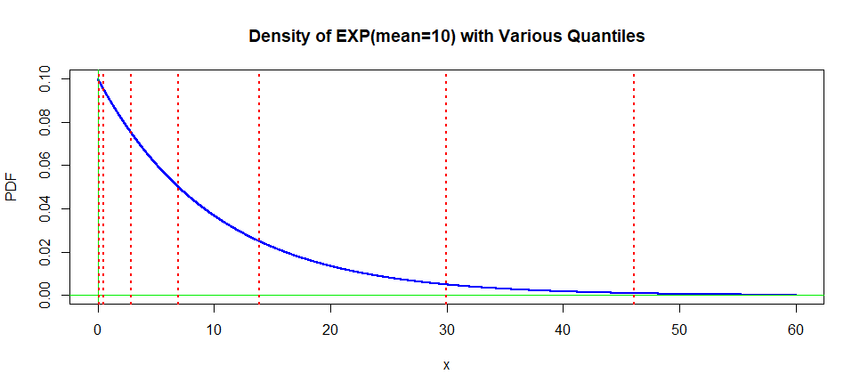
Note: All of the above is about quantiles for a normal distribution because your question deals only with normal distributions. But @Nick Cox makes a good point that quantiles are used similarly for other distributions. For example, here is a plot of an exponential distribution that has rate $\lambda = 0.1$ (hence mean $\mu = 10),$ with vertical lines at the same quantiles used above for the normal distribution.

q = round(qexp(c(.01,.05,.25,.50,.75,.95,.99), 0.1),3);  q
[1]  0.101  0.513  2.877  6.931 13.863 29.957 46.052

curve(dexp(x, 0.1), 0, 60, col="blue", lwd=2, ylab="PDF", n=10001,
      main="Density of EXP(mean=10) with Various Quantiles")
  abline(h=0, col="green2");  abline(v=0, col="green2")
  abline(v=q, col="red", lty="dotted", lwd=2)