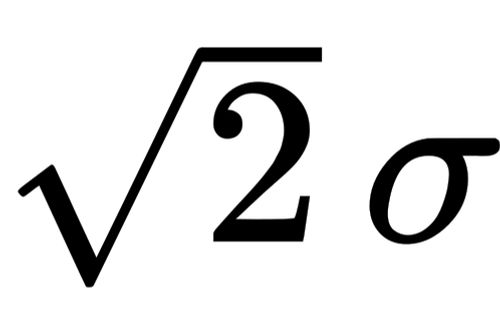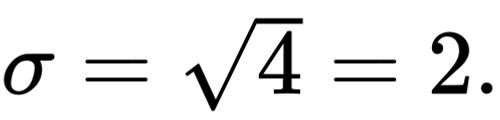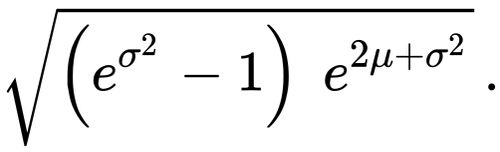dispersion of the values of a random variable around its expected value
Videos
[SOLVED by u/BurkeyAcademy]
Hello, could you review the following logic:
I designed an item with a length of 5.00 metre. After manufacturing, I collected data of hundreds of lengths of the item:
Mean = 5.10m (i.e. average 0.10m longer) Standard deviation = 0.30m
My view is that we cannot trust the 0.10m value, because the standard deviation is 0.30m. However, I looked up how to justify variability, and found Coefficient of Variability (CV) which is based on SD/mean.
Also, are there any way I can assess SD against the 0.10m value?
As other users have mentioned in the comments, "small" and "large" are arbitrary and depend on the context. However, one very simple way to think about whether a standard deviation is small or large is as follows. If you assume that your data is normally distributed, then approximately 68% of your data points fall between one standard deviation below the mean, and one standard deviation above the mean. In the case of your data, this would mean 68% of students scored between roughly 63 and 95, and conversely 32% scored either above 95 or below 63. This gives a practical way to understand what your standard deviation is telling you (again, under the assumption that your data is normal). If you would have expected a greater percentage to fall between 63 and 95, then your standard deviation may be considered large, and if you would have expected a smaller percentage, then your standard deviation may be considered small.
I believe that standard deviation is a tool to compare two data sets or more. Thus, the higher standard deviation of dataset will be the one considered large where data are more spread-out in relationships to the mean. On the other hand, a lower standard deviation will be considered small.
Also, it is a tool to evaluate how the numbers are spread-out from one data set.
the standard deviation could be considered big or small based on whatever reason the data set is serving. Example salaries of entry-level jobs, run-time of one mile for a particular sport team. for the sport team, you may have one athlete that is way faster than the others. Thus, we can use standard deviation to see how far he is above the mean. bottom line. it depends on how you want to use your data. If you think it is small, it is small. if you think it is big, it i